外卖配送路径规划算法:两阶段快速启发式算法
外卖配送是运筹优化算法重要应用领域,它的主要特点是并发高、延时低,为了解决这样的问题需要对业务进行深入理解,设计定制化优化手段。paper(A Two-Stage Fast Heuristic for Food Delivery Route Planning Problem)是2019年发表的一篇关于外卖配送路径规划的文章,十分接地气,接下来本文将对这篇文章做一番解读。
在外卖场景,用户在外卖平台点单之后,订单信息会推送至商家确认接单,之后进入履约环节。调度系统对订单进行指派和路径规划,外卖配送员根据订单指派完成取餐和送餐任务。
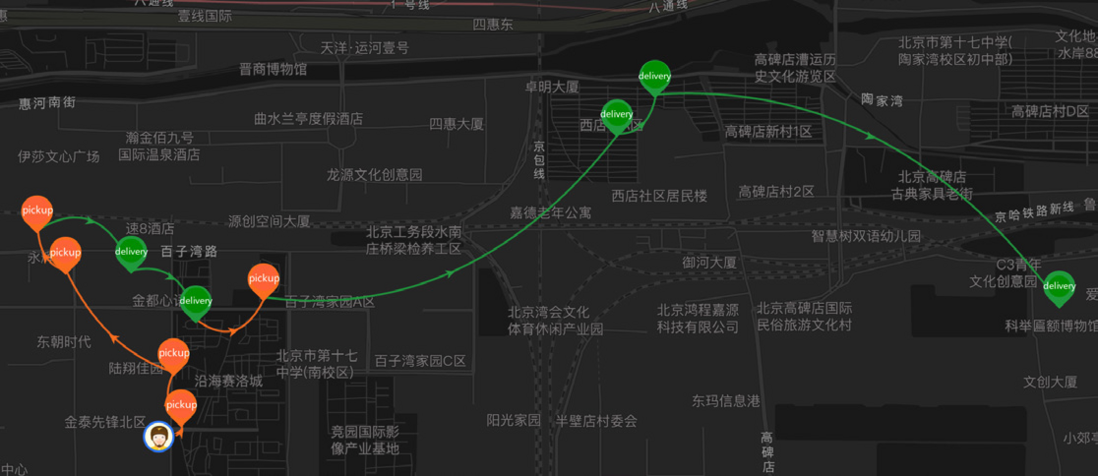
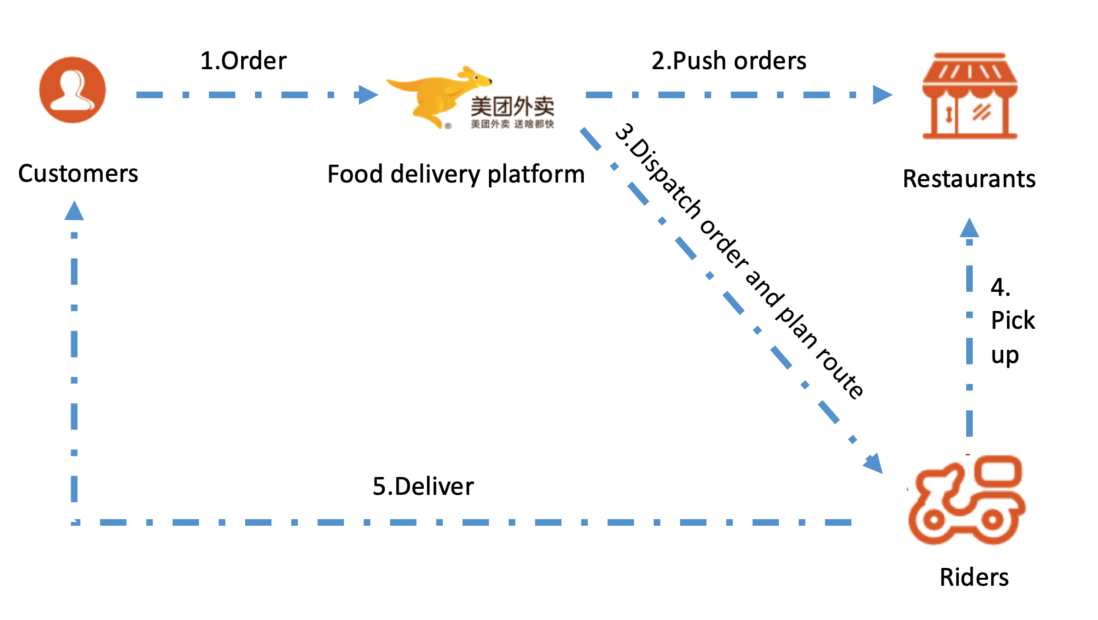 而在配送问题中,路径规划是基本且重要的一个环节,它直接决定骑手服务路线的长度和时间,从而对订单的准时率、客户满意度都产生影响。下图是配送中骑手服务的路径规划示意图,该骑手身上有5个订单,其路径规划结果为:取(4个)送(2个)取(1个)送(3个)。
而在配送问题中,路径规划是基本且重要的一个环节,它直接决定骑手服务路线的长度和时间,从而对订单的准时率、客户满意度都产生影响。下图是配送中骑手服务的路径规划示意图,该骑手身上有5个订单,其路径规划结果为:取(4个)送(2个)取(1个)送(3个)。
 目前,路径规划主要存在如下困难:计算量爆炸:由于路径规划是NP难问题,无法采用多项式算法在有限时间内求解。当问题规模增大时,计算量也呈指数增长。例如,在(午晚)高峰时刻,每个骑手身上都可能有10个以上的订单需要完成,在这种情况下,可能的路径规划结果有种,想要在有限时间内求解是极困难的。算法时效要求高:路径规划是指派算法的重要环节。指派算法是在线算法,线上会有大量的订单和骑手需要进行匹配,因此路径规划算法需要在极短时间内得到结果(毫秒级)
学界与配送场景下的路径规划问题相关的研究主要集中于PDPTW问题(pickup and delivery problem with time-windows),它考虑多个骑手和多个客户,每个客户的订单包含一个取点与一个送点,骑手按规定顺序访问各个节点完成订单的服务,从而达到某些目标函数(例如总行驶距离)的最优。求解PDPTW问题的算法包括:列生成算法(column generation)、分支切割(branch-and-cut)、分支切割定价(branch-and-cut-and-price)等精确计算算法,禁忌搜索(tabu search)、模拟退火(simulated annealing algorithm)、基于插入搜索的算法(insertion-based heuristic)、自适应大邻域搜索(adaptive large neighborhood search)、变深度搜索(variable-depth search algorithm)。由于在配送场景下,对算法时效性有极高的要求,上述算法均无法适用于配送场景的问题。在后文中,我们将介绍路径规划的问题模型,以及提出的启发式算法(Two-Stage Fast Heuristic),同时给出了一些仿真结果。
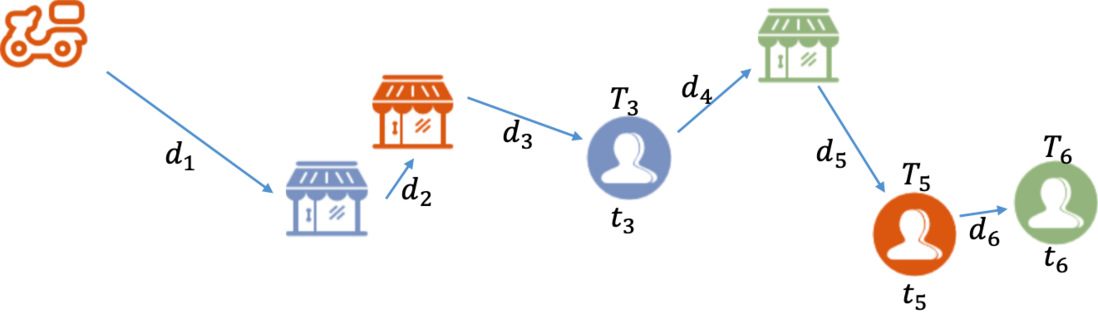
背景中提到的配送场景下的路径规划问题可以被简化建模成单车辆PDPTW问题(single vehicle pickup and delivery problem with time-windows),即原PDPTW问题的单车辆简化(仅有一个骑手)。下图表示单车辆PDPTW问题研究中的一条典型路径。其中为每个送点的预计送达时间(ETA,Estimated Time of Arrival),当订单产生时,即被告知给商家和客户。表示预估送达时间(ETR,Estimated Time of Route),由路径规划算法计算得出。为点到点的距离。
目前,路径规划主要存在如下困难:计算量爆炸:由于路径规划是NP难问题,无法采用多项式算法在有限时间内求解。当问题规模增大时,计算量也呈指数增长。例如,在(午晚)高峰时刻,每个骑手身上都可能有10个以上的订单需要完成,在这种情况下,可能的路径规划结果有种,想要在有限时间内求解是极困难的。算法时效要求高:路径规划是指派算法的重要环节。指派算法是在线算法,线上会有大量的订单和骑手需要进行匹配,因此路径规划算法需要在极短时间内得到结果(毫秒级)
学界与配送场景下的路径规划问题相关的研究主要集中于PDPTW问题(pickup and delivery problem with time-windows),它考虑多个骑手和多个客户,每个客户的订单包含一个取点与一个送点,骑手按规定顺序访问各个节点完成订单的服务,从而达到某些目标函数(例如总行驶距离)的最优。求解PDPTW问题的算法包括:列生成算法(column generation)、分支切割(branch-and-cut)、分支切割定价(branch-and-cut-and-price)等精确计算算法,禁忌搜索(tabu search)、模拟退火(simulated annealing algorithm)、基于插入搜索的算法(insertion-based heuristic)、自适应大邻域搜索(adaptive large neighborhood search)、变深度搜索(variable-depth search algorithm)。由于在配送场景下,对算法时效性有极高的要求,上述算法均无法适用于配送场景的问题。在后文中,我们将介绍路径规划的问题模型,以及提出的启发式算法(Two-Stage Fast Heuristic),同时给出了一些仿真结果。
背景中提到的配送场景下的路径规划问题可以被简化建模成单车辆PDPTW问题(single vehicle pickup and delivery problem with time-windows),即原PDPTW问题的单车辆简化(仅有一个骑手)。下图表示单车辆PDPTW问题研究中的一条典型路径。其中为每个送点的预计送达时间(ETA,Estimated Time of Arrival),当订单产生时,即被告知给商家和客户。表示预估送达时间(ETR,Estimated Time of Route),由路径规划算法计算得出。为点到点的距离。
 本文中我们考虑最小化订单超时时间与路径长度,即目标函数为
本文中我们考虑最小化订单超时时间与路径长度,即目标函数为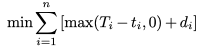 ,该问题有两个约束:优先约束:订单的取点需在送点前访问容量约束:骑手在服务过程中同时携带的订单数量具有上限
TSFH(Two-Stage Fast Heuristic)主要包括两个阶段stage I:初始化得到一个初始可行解采用贪婪插入策略与基于地理信息的加速策略stage II:对初始解进行邻域搜索两种邻域分别对“最超时”和“最不超时”订单进行调整3.1.1贪婪插入初始化
,该问题有两个约束:优先约束:订单的取点需在送点前访问容量约束:骑手在服务过程中同时携带的订单数量具有上限
TSFH(Two-Stage Fast Heuristic)主要包括两个阶段stage I:初始化得到一个初始可行解采用贪婪插入策略与基于地理信息的加速策略stage II:对初始解进行邻域搜索两种邻域分别对“最超时”和“最不超时”订单进行调整3.1.1贪婪插入初始化
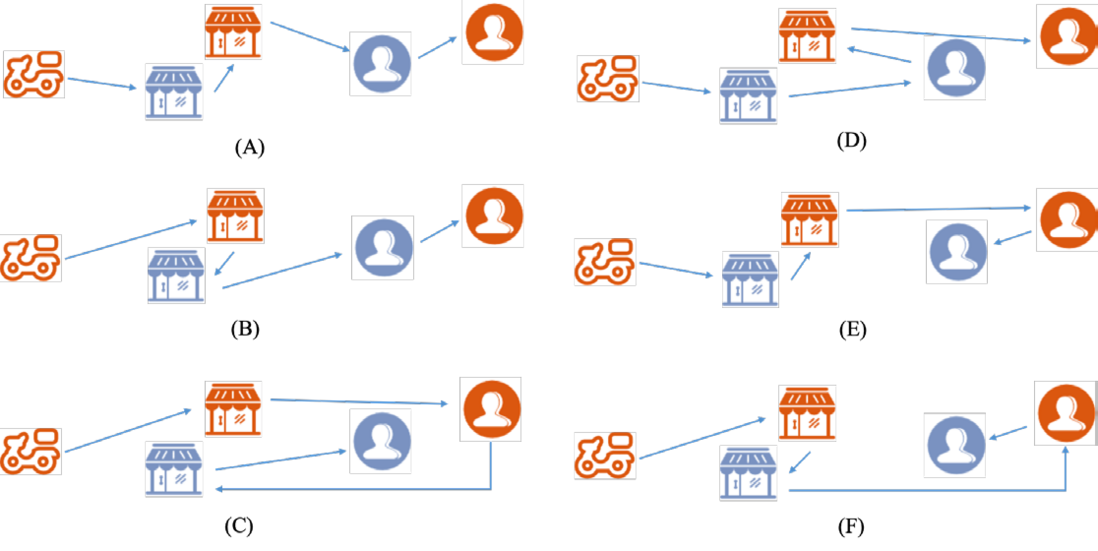 贪婪插入初始化主要包括以下步骤:订单按照ETA时间升序排序;取出第一个订单,进行排序。注意收到优先约束的影响,只有一种排列方法(取点在送点前);对剩余的订单,按顺序将其取送点插入所有可能位置,找到最优位置(目标函数最小),将其插入。
下图为初始化中贪婪插入的一个例子,在插入第二个订单时,我们有6种插入方案,根据目标函数最小原则,(A)为最优插入方案。
当所有点都完成插入后,便得到一个可行解。3.1.2基于地理信息的加速策略
观察商家和客户的地理信息可以发现,商家之间可能距离很近(例如中心商业区域所含的商家可能服务半径5km以内的60%的客户),客户也是如此(多个客户可能位于同一个小区或楼宇)。因此我们可以通过分层聚类的方法将取送点聚类为不同的集群,通过对这些集群进行分析,我们可以减少无效插入,提高贪婪插入初始化的速度。根据引理1,2可以得到加速策略如下:若节点j被分到组i,则最好的插入策略是将其插入组i,或是组i之后的组之间。
下面分别介绍聚类算法以及相关引理。
【聚类算法】 令D为聚类范围(例如D=100m),按照以下逻辑对各个节点进行聚类:若节点未被分类,则节点产生一个新组,并变成该组的中心点对于一个节点,如果节点没有被分类,且,则被分到组若节点被分到组,且不是中心点,如果,则将重新分至组
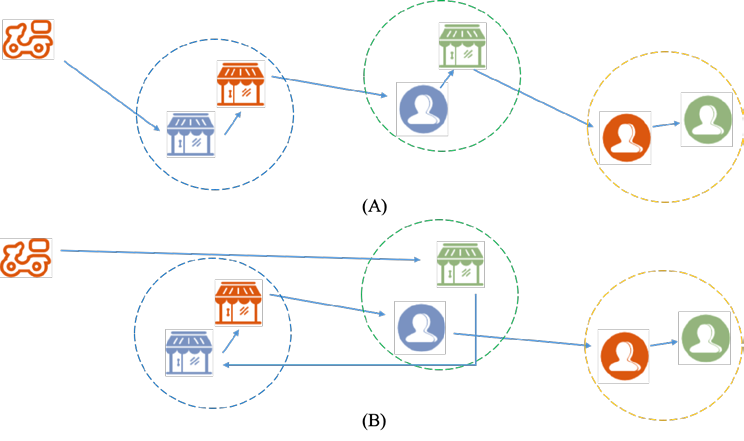
【Lemma 1】将节点插入所在组之前的组: 如果节点被分至组,则将节点插入到组之前的任何组一定劣于将节点插入组
Proof: 节点属于组,则将节点插入到组之前的任何组一定不如将节点直接插入组,因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设蓝色组与橙色组的点已经完成插入,我们考虑绿色组的节点的插入。从图中可以看到,将节点插入所在组之前的组(B)总是比插入自己所在的组(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
贪婪插入初始化主要包括以下步骤:订单按照ETA时间升序排序;取出第一个订单,进行排序。注意收到优先约束的影响,只有一种排列方法(取点在送点前);对剩余的订单,按顺序将其取送点插入所有可能位置,找到最优位置(目标函数最小),将其插入。
下图为初始化中贪婪插入的一个例子,在插入第二个订单时,我们有6种插入方案,根据目标函数最小原则,(A)为最优插入方案。
当所有点都完成插入后,便得到一个可行解。3.1.2基于地理信息的加速策略
观察商家和客户的地理信息可以发现,商家之间可能距离很近(例如中心商业区域所含的商家可能服务半径5km以内的60%的客户),客户也是如此(多个客户可能位于同一个小区或楼宇)。因此我们可以通过分层聚类的方法将取送点聚类为不同的集群,通过对这些集群进行分析,我们可以减少无效插入,提高贪婪插入初始化的速度。根据引理1,2可以得到加速策略如下:若节点j被分到组i,则最好的插入策略是将其插入组i,或是组i之后的组之间。
下面分别介绍聚类算法以及相关引理。
【聚类算法】 令D为聚类范围(例如D=100m),按照以下逻辑对各个节点进行聚类:若节点未被分类,则节点产生一个新组,并变成该组的中心点对于一个节点,如果节点没有被分类,且,则被分到组若节点被分到组,且不是中心点,如果,则将重新分至组
【Lemma 1】将节点插入所在组之前的组: 如果节点被分至组,则将节点插入到组之前的任何组一定劣于将节点插入组
Proof: 节点属于组,则将节点插入到组之前的任何组一定不如将节点直接插入组,因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设蓝色组与橙色组的点已经完成插入,我们考虑绿色组的节点的插入。从图中可以看到,将节点插入所在组之前的组(B)总是比插入自己所在的组(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
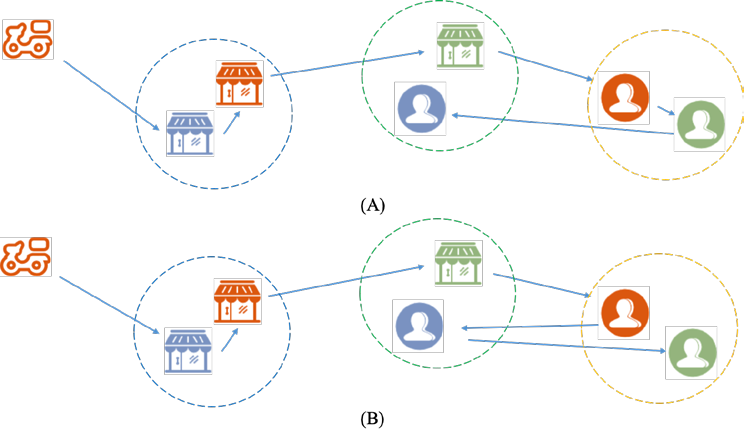
 【Lemma 2】将节点插入所在组之后的组: 如果节点被分至组,则我们总可以找到一个插入方案优于将节点插入到组之后的组
Proof: 节点属于组,则将节点插入到组之后的组一定不如将节点插入组和组之间(如果是最后一个组,则插入到最后位置),因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设橙色组与绿色组的点已经完成插入,我们考虑蓝色组的节点的插入。从图中可以看到,将节点插入所在组之后的组之间(B)一定比插入到最后位置(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
【Lemma 2】将节点插入所在组之后的组: 如果节点被分至组,则我们总可以找到一个插入方案优于将节点插入到组之后的组
Proof: 节点属于组,则将节点插入到组之后的组一定不如将节点插入组和组之间(如果是最后一个组,则插入到最后位置),因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设橙色组与绿色组的点已经完成插入,我们考虑蓝色组的节点的插入。从图中可以看到,将节点插入所在组之后的组之间(B)一定比插入到最后位置(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
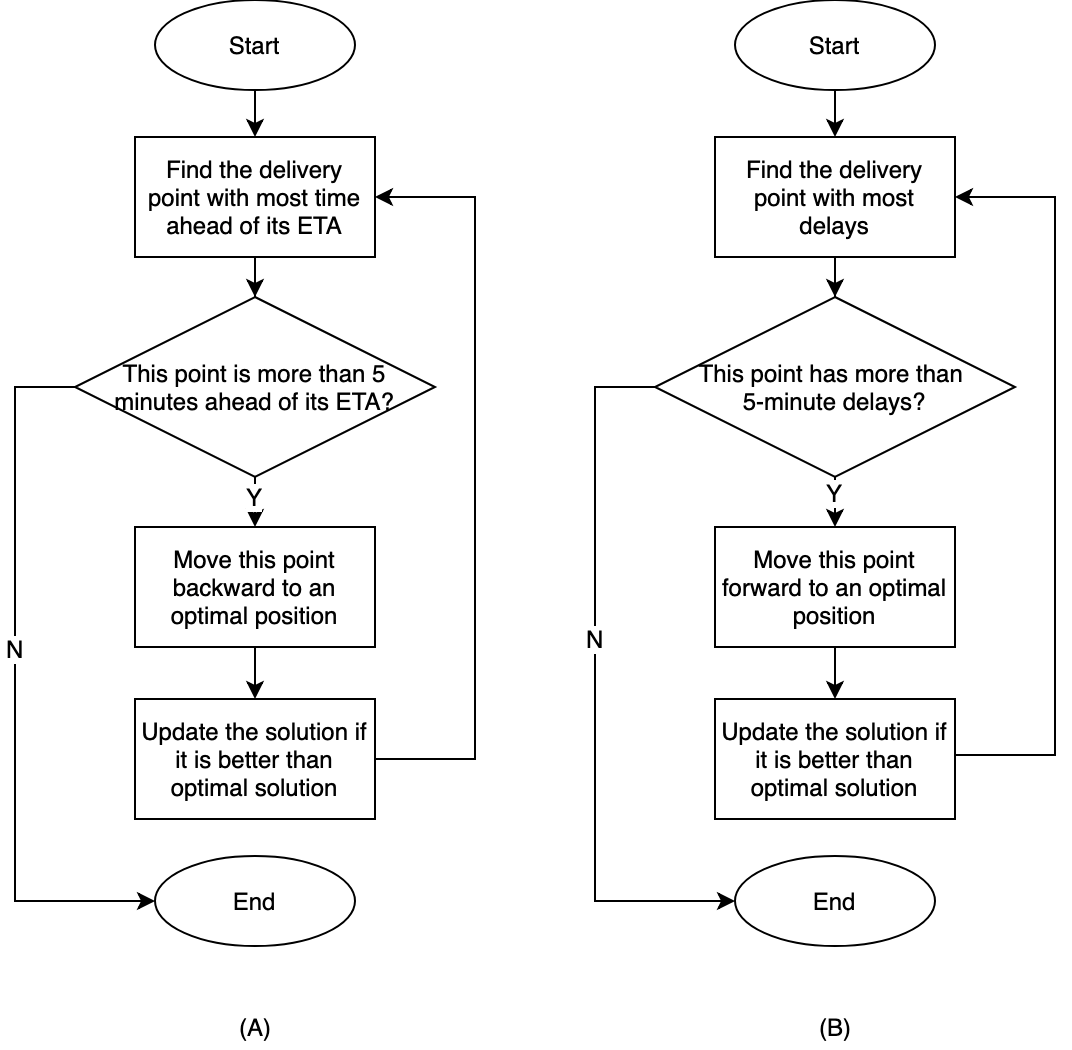
 在初始化结束后,局部搜索通过在初始解的邻域范围内进行搜索来提高解的质量。我们的算法考虑两种类型的邻域:找到提前最多的节点,将其后移,插入最优位置。流程如下图A所示。找到超时最多的节点,将其前移,插入最优位置。流程如下图B所示。
注:每次局部搜索找到一个更好的解时,当前最优解即被替换。
在初始化结束后,局部搜索通过在初始解的邻域范围内进行搜索来提高解的质量。我们的算法考虑两种类型的邻域:找到提前最多的节点,将其后移,插入最优位置。流程如下图A所示。找到超时最多的节点,将其前移,插入最优位置。流程如下图B所示。
注:每次局部搜索找到一个更好的解时,当前最优解即被替换。
 本节给出一些仿真结果。首先我们比较了带有加速策略初始化与不带加速策略初始化的结果,以验证初始化中加速策略的有效性。之后,我们将TSFH产生的解与暴力算法得到的最优解进行比较,从而验证TSFH产生近似最优解的能力。最后,我们将TSFH与目前最好的一些算法进行比较,验证TSFH求解该问题的有效性。
算例从实际路径规划问题中均匀采样得到,根据取送点的数量分为三类:“<10”, "10-20", ">20"。
算法的评价指标采用总分(Total Score)和平均时间(Average Time)。总分为超时时间与路径长度的和,平均时间为一个算例的平均运行时间。
运行环境为MacBook Pro with 2.2 GHz processors / 16 GB RAM in Mac-OS,编程语言为Java,IDE为Eclipse。
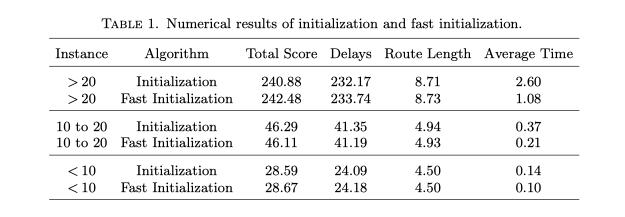
表一为带有加速策略初始化与不带加速策略初始化的比较结果。可以看出,加速策略有着明显的效果。例如"10-20"算例的平均运行时间从0.37降至0.21,减少了43.2%。同时,从总分可以看出,加速策略初始化的效果几乎没有受到影响,这证明加速策略不会以牺牲解的质量为代价,可以在短时间内产生优良解。
本节给出一些仿真结果。首先我们比较了带有加速策略初始化与不带加速策略初始化的结果,以验证初始化中加速策略的有效性。之后,我们将TSFH产生的解与暴力算法得到的最优解进行比较,从而验证TSFH产生近似最优解的能力。最后,我们将TSFH与目前最好的一些算法进行比较,验证TSFH求解该问题的有效性。
算例从实际路径规划问题中均匀采样得到,根据取送点的数量分为三类:“<10”, "10-20", ">20"。
算法的评价指标采用总分(Total Score)和平均时间(Average Time)。总分为超时时间与路径长度的和,平均时间为一个算例的平均运行时间。
运行环境为MacBook Pro with 2.2 GHz processors / 16 GB RAM in Mac-OS,编程语言为Java,IDE为Eclipse。
表一为带有加速策略初始化与不带加速策略初始化的比较结果。可以看出,加速策略有着明显的效果。例如"10-20"算例的平均运行时间从0.37降至0.21,减少了43.2%。同时,从总分可以看出,加速策略初始化的效果几乎没有受到影响,这证明加速策略不会以牺牲解的质量为代价,可以在短时间内产生优良解。
 问题规模较小时,该问题的最优解可以通过暴力搜索算法来得到。考虑n个取点和n个送点,不考虑容量约束的条件下,暴力搜索算法的复杂度为
问题规模较小时,该问题的最优解可以通过暴力搜索算法来得到。考虑n个取点和n个送点,不考虑容量约束的条件下,暴力搜索算法的复杂度为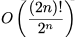 。这里我们只提供“<10”算例的比较结果如表二。
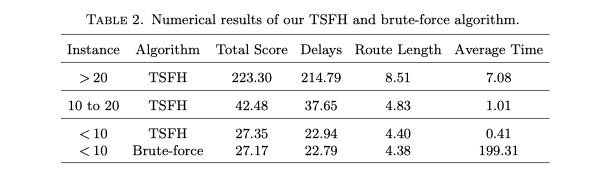
可以看出,对于“<10”的算例,TSFH仅需暴力算法运行时间的0.21%,即可达到几乎一样的效果。另外,“10-20”与“>20”算例的运行时间也均在毫秒级。在现实中,大部分情况都可被“<10”和“10-20”的算例覆盖,因此这表明TSFH足以在毫秒数量级内解决配送中的路径规划问题。
。这里我们只提供“<10”算例的比较结果如表二。
可以看出,对于“<10”的算例,TSFH仅需暴力算法运行时间的0.21%,即可达到几乎一样的效果。另外,“10-20”与“>20”算例的运行时间也均在毫秒级。在现实中,大部分情况都可被“<10”和“10-20”的算例覆盖,因此这表明TSFH足以在毫秒数量级内解决配送中的路径规划问题。
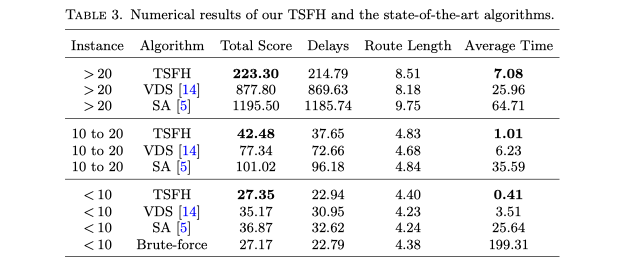
 TSFH与variable-depth search (VDS)、simulated annealing (SA)的比较结果如表三。可以看出TSFH在总分和平均时间两方面都优于VDS和SA。在“<10”算例中,TSFH达到了近似最优解,仅比最优解高0.7%,而VDS和SA分别高了29.4%和35.7%。另外,TSFH求解“<10”算例的平均时间为0.41ms,而VDS和SA分别为3.51ms和25.64ms。配送环境中的路径规划对于算法的运行速度有着极高的要求,TSFH可以在1ms内完成“<10”算例的求解,而VDS和SA的运行时间均无法接受。因此,TSFH是比VDS和SA更好更有效的算法,也更适用于配送环境下的路径规划问题求解。
TSFH与variable-depth search (VDS)、simulated annealing (SA)的比较结果如表三。可以看出TSFH在总分和平均时间两方面都优于VDS和SA。在“<10”算例中,TSFH达到了近似最优解,仅比最优解高0.7%,而VDS和SA分别高了29.4%和35.7%。另外,TSFH求解“<10”算例的平均时间为0.41ms,而VDS和SA分别为3.51ms和25.64ms。配送环境中的路径规划对于算法的运行速度有着极高的要求,TSFH可以在1ms内完成“<10”算例的求解,而VDS和SA的运行时间均无法接受。因此,TSFH是比VDS和SA更好更有效的算法,也更适用于配送环境下的路径规划问题求解。
 本篇文章将外卖配送环境下的路径规划问题建模为单车辆PDPTW问题。与传统求解单车辆PDPTW问题的算法不同,本篇提出了一种两阶段快速启发式算法(TSFH)。在第一阶段,通过贪婪初始化得到一个可行的优良解。根据顾客和商户的地理位置信息,设计了一种加速策略,在节点调整时避免了无效插入。在第二阶段,通过在当前解的两种邻域内进行搜索,解的质量得到了进一步提升。
仿真结果表明,TSFH与暴力搜索算法、VDS、SA相比,在解的质量和运行时间方面均有着极大的优势。同时,TSFH具备在毫秒数量级内产生近似最优解的能力,适用于配送场景下路径规划问题的求解。
本篇文章将外卖配送环境下的路径规划问题建模为单车辆PDPTW问题。与传统求解单车辆PDPTW问题的算法不同,本篇提出了一种两阶段快速启发式算法(TSFH)。在第一阶段,通过贪婪初始化得到一个可行的优良解。根据顾客和商户的地理位置信息,设计了一种加速策略,在节点调整时避免了无效插入。在第二阶段,通过在当前解的两种邻域内进行搜索,解的质量得到了进一步提升。
仿真结果表明,TSFH与暴力搜索算法、VDS、SA相比,在解的质量和运行时间方面均有着极大的优势。同时,TSFH具备在毫秒数量级内产生近似最优解的能力,适用于配送场景下路径规划问题的求解。
 而在配送问题中,路径规划是基本且重要的一个环节,它直接决定骑手服务路线的长度和时间,从而对订单的准时率、客户满意度都产生影响。下图是配送中骑手服务的路径规划示意图,该骑手身上有5个订单,其路径规划结果为:取(4个)送(2个)取(1个)送(3个)。
而在配送问题中,路径规划是基本且重要的一个环节,它直接决定骑手服务路线的长度和时间,从而对订单的准时率、客户满意度都产生影响。下图是配送中骑手服务的路径规划示意图,该骑手身上有5个订单,其路径规划结果为:取(4个)送(2个)取(1个)送(3个)。
 目前,路径规划主要存在如下困难:计算量爆炸:由于路径规划是NP难问题,无法采用多项式算法在有限时间内求解。当问题规模增大时,计算量也呈指数增长。例如,在(午晚)高峰时刻,每个骑手身上都可能有10个以上的订单需要完成,在这种情况下,可能的路径规划结果有种,想要在有限时间内求解是极困难的。算法时效要求高:路径规划是指派算法的重要环节。指派算法是在线算法,线上会有大量的订单和骑手需要进行匹配,因此路径规划算法需要在极短时间内得到结果(毫秒级)
学界与配送场景下的路径规划问题相关的研究主要集中于PDPTW问题(pickup and delivery problem with time-windows),它考虑多个骑手和多个客户,每个客户的订单包含一个取点与一个送点,骑手按规定顺序访问各个节点完成订单的服务,从而达到某些目标函数(例如总行驶距离)的最优。求解PDPTW问题的算法包括:列生成算法(column generation)、分支切割(branch-and-cut)、分支切割定价(branch-and-cut-and-price)等精确计算算法,禁忌搜索(tabu search)、模拟退火(simulated annealing algorithm)、基于插入搜索的算法(insertion-based heuristic)、自适应大邻域搜索(adaptive large neighborhood search)、变深度搜索(variable-depth search algorithm)。由于在配送场景下,对算法时效性有极高的要求,上述算法均无法适用于配送场景的问题。在后文中,我们将介绍路径规划的问题模型,以及提出的启发式算法(Two-Stage Fast Heuristic),同时给出了一些仿真结果。
背景中提到的配送场景下的路径规划问题可以被简化建模成单车辆PDPTW问题(single vehicle pickup and delivery problem with time-windows),即原PDPTW问题的单车辆简化(仅有一个骑手)。下图表示单车辆PDPTW问题研究中的一条典型路径。其中为每个送点的预计送达时间(ETA,Estimated Time of Arrival),当订单产生时,即被告知给商家和客户。表示预估送达时间(ETR,Estimated Time of Route),由路径规划算法计算得出。为点到点的距离。
目前,路径规划主要存在如下困难:计算量爆炸:由于路径规划是NP难问题,无法采用多项式算法在有限时间内求解。当问题规模增大时,计算量也呈指数增长。例如,在(午晚)高峰时刻,每个骑手身上都可能有10个以上的订单需要完成,在这种情况下,可能的路径规划结果有种,想要在有限时间内求解是极困难的。算法时效要求高:路径规划是指派算法的重要环节。指派算法是在线算法,线上会有大量的订单和骑手需要进行匹配,因此路径规划算法需要在极短时间内得到结果(毫秒级)
学界与配送场景下的路径规划问题相关的研究主要集中于PDPTW问题(pickup and delivery problem with time-windows),它考虑多个骑手和多个客户,每个客户的订单包含一个取点与一个送点,骑手按规定顺序访问各个节点完成订单的服务,从而达到某些目标函数(例如总行驶距离)的最优。求解PDPTW问题的算法包括:列生成算法(column generation)、分支切割(branch-and-cut)、分支切割定价(branch-and-cut-and-price)等精确计算算法,禁忌搜索(tabu search)、模拟退火(simulated annealing algorithm)、基于插入搜索的算法(insertion-based heuristic)、自适应大邻域搜索(adaptive large neighborhood search)、变深度搜索(variable-depth search algorithm)。由于在配送场景下,对算法时效性有极高的要求,上述算法均无法适用于配送场景的问题。在后文中,我们将介绍路径规划的问题模型,以及提出的启发式算法(Two-Stage Fast Heuristic),同时给出了一些仿真结果。
背景中提到的配送场景下的路径规划问题可以被简化建模成单车辆PDPTW问题(single vehicle pickup and delivery problem with time-windows),即原PDPTW问题的单车辆简化(仅有一个骑手)。下图表示单车辆PDPTW问题研究中的一条典型路径。其中为每个送点的预计送达时间(ETA,Estimated Time of Arrival),当订单产生时,即被告知给商家和客户。表示预估送达时间(ETR,Estimated Time of Route),由路径规划算法计算得出。为点到点的距离。
 本文中我们考虑最小化订单超时时间与路径长度,即目标函数为
本文中我们考虑最小化订单超时时间与路径长度,即目标函数为 贪婪插入初始化主要包括以下步骤:订单按照ETA时间升序排序;取出第一个订单,进行排序。注意收到优先约束的影响,只有一种排列方法(取点在送点前);对剩余的订单,按顺序将其取送点插入所有可能位置,找到最优位置(目标函数最小),将其插入。
下图为初始化中贪婪插入的一个例子,在插入第二个订单时,我们有6种插入方案,根据目标函数最小原则,(A)为最优插入方案。
当所有点都完成插入后,便得到一个可行解。3.1.2基于地理信息的加速策略
观察商家和客户的地理信息可以发现,商家之间可能距离很近(例如中心商业区域所含的商家可能服务半径5km以内的60%的客户),客户也是如此(多个客户可能位于同一个小区或楼宇)。因此我们可以通过分层聚类的方法将取送点聚类为不同的集群,通过对这些集群进行分析,我们可以减少无效插入,提高贪婪插入初始化的速度。根据引理1,2可以得到加速策略如下:若节点j被分到组i,则最好的插入策略是将其插入组i,或是组i之后的组之间。
下面分别介绍聚类算法以及相关引理。
【聚类算法】 令D为聚类范围(例如D=100m),按照以下逻辑对各个节点进行聚类:若节点未被分类,则节点产生一个新组,并变成该组的中心点对于一个节点,如果节点没有被分类,且,则被分到组若节点被分到组,且不是中心点,如果,则将重新分至组
【Lemma 1】将节点插入所在组之前的组: 如果节点被分至组,则将节点插入到组之前的任何组一定劣于将节点插入组
Proof: 节点属于组,则将节点插入到组之前的任何组一定不如将节点直接插入组,因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设蓝色组与橙色组的点已经完成插入,我们考虑绿色组的节点的插入。从图中可以看到,将节点插入所在组之前的组(B)总是比插入自己所在的组(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
贪婪插入初始化主要包括以下步骤:订单按照ETA时间升序排序;取出第一个订单,进行排序。注意收到优先约束的影响,只有一种排列方法(取点在送点前);对剩余的订单,按顺序将其取送点插入所有可能位置,找到最优位置(目标函数最小),将其插入。
下图为初始化中贪婪插入的一个例子,在插入第二个订单时,我们有6种插入方案,根据目标函数最小原则,(A)为最优插入方案。
当所有点都完成插入后,便得到一个可行解。3.1.2基于地理信息的加速策略
观察商家和客户的地理信息可以发现,商家之间可能距离很近(例如中心商业区域所含的商家可能服务半径5km以内的60%的客户),客户也是如此(多个客户可能位于同一个小区或楼宇)。因此我们可以通过分层聚类的方法将取送点聚类为不同的集群,通过对这些集群进行分析,我们可以减少无效插入,提高贪婪插入初始化的速度。根据引理1,2可以得到加速策略如下:若节点j被分到组i,则最好的插入策略是将其插入组i,或是组i之后的组之间。
下面分别介绍聚类算法以及相关引理。
【聚类算法】 令D为聚类范围(例如D=100m),按照以下逻辑对各个节点进行聚类:若节点未被分类,则节点产生一个新组,并变成该组的中心点对于一个节点,如果节点没有被分类,且,则被分到组若节点被分到组,且不是中心点,如果,则将重新分至组
【Lemma 1】将节点插入所在组之前的组: 如果节点被分至组,则将节点插入到组之前的任何组一定劣于将节点插入组
Proof: 节点属于组,则将节点插入到组之前的任何组一定不如将节点直接插入组,因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设蓝色组与橙色组的点已经完成插入,我们考虑绿色组的节点的插入。从图中可以看到,将节点插入所在组之前的组(B)总是比插入自己所在的组(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
 【Lemma 2】将节点插入所在组之后的组: 如果节点被分至组,则我们总可以找到一个插入方案优于将节点插入到组之后的组
Proof: 节点属于组,则将节点插入到组之后的组一定不如将节点插入组和组之间(如果是最后一个组,则插入到最后位置),因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设橙色组与绿色组的点已经完成插入,我们考虑蓝色组的节点的插入。从图中可以看到,将节点插入所在组之后的组之间(B)一定比插入到最后位置(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
【Lemma 2】将节点插入所在组之后的组: 如果节点被分至组,则我们总可以找到一个插入方案优于将节点插入到组之后的组
Proof: 节点属于组,则将节点插入到组之后的组一定不如将节点插入组和组之间(如果是最后一个组,则插入到最后位置),因为路径长度变长了,但no delivery point benefits from shorter delays.
下图给出了一个例子,取点和送点被分成了三个组,假设橙色组与绿色组的点已经完成插入,我们考虑蓝色组的节点的插入。从图中可以看到,将节点插入所在组之后的组之间(B)一定比插入到最后位置(A)更差,因为骑手路径长度变长,客户处可能会出现更高的超时。
 在初始化结束后,局部搜索通过在初始解的邻域范围内进行搜索来提高解的质量。我们的算法考虑两种类型的邻域:找到提前最多的节点,将其后移,插入最优位置。流程如下图A所示。找到超时最多的节点,将其前移,插入最优位置。流程如下图B所示。
注:每次局部搜索找到一个更好的解时,当前最优解即被替换。
在初始化结束后,局部搜索通过在初始解的邻域范围内进行搜索来提高解的质量。我们的算法考虑两种类型的邻域:找到提前最多的节点,将其后移,插入最优位置。流程如下图A所示。找到超时最多的节点,将其前移,插入最优位置。流程如下图B所示。
注:每次局部搜索找到一个更好的解时,当前最优解即被替换。
 本节给出一些仿真结果。首先我们比较了带有加速策略初始化与不带加速策略初始化的结果,以验证初始化中加速策略的有效性。之后,我们将TSFH产生的解与暴力算法得到的最优解进行比较,从而验证TSFH产生近似最优解的能力。最后,我们将TSFH与目前最好的一些算法进行比较,验证TSFH求解该问题的有效性。
算例从实际路径规划问题中均匀采样得到,根据取送点的数量分为三类:“<10”, "10-20", ">20"。
算法的评价指标采用总分(Total Score)和平均时间(Average Time)。总分为超时时间与路径长度的和,平均时间为一个算例的平均运行时间。
运行环境为MacBook Pro with 2.2 GHz processors / 16 GB RAM in Mac-OS,编程语言为Java,IDE为Eclipse。
表一为带有加速策略初始化与不带加速策略初始化的比较结果。可以看出,加速策略有着明显的效果。例如"10-20"算例的平均运行时间从0.37降至0.21,减少了43.2%。同时,从总分可以看出,加速策略初始化的效果几乎没有受到影响,这证明加速策略不会以牺牲解的质量为代价,可以在短时间内产生优良解。
本节给出一些仿真结果。首先我们比较了带有加速策略初始化与不带加速策略初始化的结果,以验证初始化中加速策略的有效性。之后,我们将TSFH产生的解与暴力算法得到的最优解进行比较,从而验证TSFH产生近似最优解的能力。最后,我们将TSFH与目前最好的一些算法进行比较,验证TSFH求解该问题的有效性。
算例从实际路径规划问题中均匀采样得到,根据取送点的数量分为三类:“<10”, "10-20", ">20"。
算法的评价指标采用总分(Total Score)和平均时间(Average Time)。总分为超时时间与路径长度的和,平均时间为一个算例的平均运行时间。
运行环境为MacBook Pro with 2.2 GHz processors / 16 GB RAM in Mac-OS,编程语言为Java,IDE为Eclipse。
表一为带有加速策略初始化与不带加速策略初始化的比较结果。可以看出,加速策略有着明显的效果。例如"10-20"算例的平均运行时间从0.37降至0.21,减少了43.2%。同时,从总分可以看出,加速策略初始化的效果几乎没有受到影响,这证明加速策略不会以牺牲解的质量为代价,可以在短时间内产生优良解。
 问题规模较小时,该问题的最优解可以通过暴力搜索算法来得到。考虑n个取点和n个送点,不考虑容量约束的条件下,暴力搜索算法的复杂度为
问题规模较小时,该问题的最优解可以通过暴力搜索算法来得到。考虑n个取点和n个送点,不考虑容量约束的条件下,暴力搜索算法的复杂度为 TSFH与variable-depth search (VDS)、simulated annealing (SA)的比较结果如表三。可以看出TSFH在总分和平均时间两方面都优于VDS和SA。在“<10”算例中,TSFH达到了近似最优解,仅比最优解高0.7%,而VDS和SA分别高了29.4%和35.7%。另外,TSFH求解“<10”算例的平均时间为0.41ms,而VDS和SA分别为3.51ms和25.64ms。配送环境中的路径规划对于算法的运行速度有着极高的要求,TSFH可以在1ms内完成“<10”算例的求解,而VDS和SA的运行时间均无法接受。因此,TSFH是比VDS和SA更好更有效的算法,也更适用于配送环境下的路径规划问题求解。
TSFH与variable-depth search (VDS)、simulated annealing (SA)的比较结果如表三。可以看出TSFH在总分和平均时间两方面都优于VDS和SA。在“<10”算例中,TSFH达到了近似最优解,仅比最优解高0.7%,而VDS和SA分别高了29.4%和35.7%。另外,TSFH求解“<10”算例的平均时间为0.41ms,而VDS和SA分别为3.51ms和25.64ms。配送环境中的路径规划对于算法的运行速度有着极高的要求,TSFH可以在1ms内完成“<10”算例的求解,而VDS和SA的运行时间均无法接受。因此,TSFH是比VDS和SA更好更有效的算法,也更适用于配送环境下的路径规划问题求解。
 本篇文章将外卖配送环境下的路径规划问题建模为单车辆PDPTW问题。与传统求解单车辆PDPTW问题的算法不同,本篇提出了一种两阶段快速启发式算法(TSFH)。在第一阶段,通过贪婪初始化得到一个可行的优良解。根据顾客和商户的地理位置信息,设计了一种加速策略,在节点调整时避免了无效插入。在第二阶段,通过在当前解的两种邻域内进行搜索,解的质量得到了进一步提升。
仿真结果表明,TSFH与暴力搜索算法、VDS、SA相比,在解的质量和运行时间方面均有着极大的优势。同时,TSFH具备在毫秒数量级内产生近似最优解的能力,适用于配送场景下路径规划问题的求解。
本篇文章将外卖配送环境下的路径规划问题建模为单车辆PDPTW问题。与传统求解单车辆PDPTW问题的算法不同,本篇提出了一种两阶段快速启发式算法(TSFH)。在第一阶段,通过贪婪初始化得到一个可行的优良解。根据顾客和商户的地理位置信息,设计了一种加速策略,在节点调整时避免了无效插入。在第二阶段,通过在当前解的两种邻域内进行搜索,解的质量得到了进一步提升。
仿真结果表明,TSFH与暴力搜索算法、VDS、SA相比,在解的质量和运行时间方面均有着极大的优势。同时,TSFH具备在毫秒数量级内产生近似最优解的能力,适用于配送场景下路径规划问题的求解。 版权说明:
1.版权归本网站或原作者所有;
2.未经本网或原作者允许不得转载本文内容,否则将视为侵权;
3.转载或者引用本文内容请注明来源及原作者;
4.对于不遵守此声明或者其他违法使用本文内容者,本人依法保留追究权等。



